【进阶】深度学习中的优化算法详解

# 2.1 梯度下降算法的基本原理

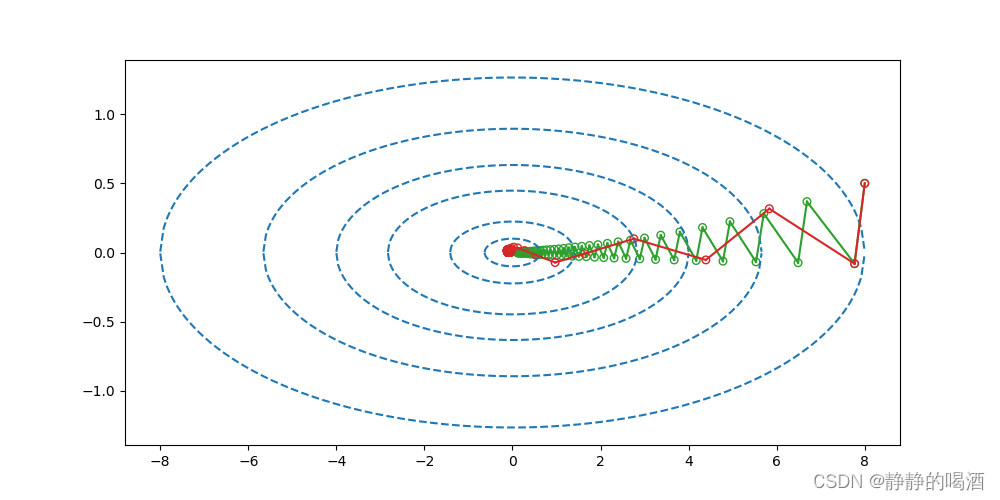
梯度下降算法是一种迭代优化算法，它通过反复更新模型参数来最小化损失函数。在每次迭代中，算法都会计算损失函数的梯度，并沿着负梯度方向更新参数。梯度下降算法的基本原理如下：

### 2.1.1 梯度下降的数学原理

给定一个损失函数 L(w)，其中 w 是模型参数，梯度下降算法通过以下公式更新参数：

w = w - α * ∇L(w)

其中：

* w 是模型参数
* α 是学习率，控制更新幅度
* ∇L(w) 是损失函数 L(w) 的梯度，它表示损失函数在 w 点的切线方向

### 2.1.2 梯度下降算法的步骤

梯度下降算法的步骤如下：

1. 初始化模型参数 w
2. 计算损失函数 L(w) 的梯度 ∇L(w)
3. 更新模型参数 w：w = w - α * ∇L(w)
4. 重复步骤 2-3，直到损失函数收敛或达到最大迭代次数

# 2. 梯度下降算法及其变种

### 2.1 梯度下降算法的基本原理

#### 2.1.1 梯度下降的数学原理

梯度下降算法是一种迭代优化算法，用于寻找函数的最小值或最大值。其基本原理是沿着函数梯度的负方向迭代更新参数，使得函数值逐渐减小或增大。

对于一个可微函数 f(x)，其梯度表示为：

∇f(x) = [∂f(x)/∂x1, ∂f(x)/∂x2, ..., ∂f(x)/∂xn]

其中，x = [x1, x2, ..., xn] 是函数的自变量。

梯度下降算法的更新公式为：

x_t+1 = x_t - α * ∇f(x_t)

其中：

* x_t 是第 t 次迭代的参数值
* x_t+1 是第 t+1 次迭代的参数值
* α 是学习率，控制更新步长

#### 2.1.2 梯度下降算法的步骤

梯度下降算法的步骤如下：

1. 初始化参数值 x_0
2. 计算函数 f(x_t) 的梯度 ∇f(x_t)
3. 更新参数值 x_t+1 = x_t - α * ∇f(x_t)
4. 重复步骤 2 和 3，直到满足终止条件（例如，达到最大迭代次数或函数值收敛）

### 2.2 梯度下降算法的变种

为了提高梯度下降算法的性能，提出了多种变种算法，包括：

#### 2.2.1 动量梯度下降（Momentum）

动量梯度下降算法在更新参数时加入了动量项，使得算法能够沿着梯度方向加速前进。其更新公式为：

v_t = β * v_t-1 + (1 - β) * ∇f(x_t)
x_t+1 = x_t - α * v_t

其中：

* v_t 是动量项
* β 是动量系数，控制动量项的衰减程度

#### 2.2.2 RMSprop

RMSprop（Root Mean Square Propagation）算法通过自适应调整学习率来提高算法的收敛速度。其更新公式为：

s_t = β * s_t-1 + (1 - β) * (∇f(x_t))^2
x_t+1 = x_t - α * ∇f(x_t) / √(s_t + ε)

其中：

* s_t 是均方根项
* β 是衰减系数，控制均方根项的衰减程度
* ε 是平滑项，防止分母为零

#### 2.2.3 Adam

Adam（Adaptive Moment Estimation）算法结合了动量和 RMSprop 算法的优点，自适应地调整学习率和动量。其更新公式为：

m_t = β1 * m_t-1 + (1 - β1) * ∇f(x_t)
v_t = β2 * v_t-1 + (1 - β2) * (∇f(x_t))^2
x_t+1 = x_t - α * m_t / √(v_t + ε)

其中：

* m_t 是动量项
* v_t 是均方根项
* β1 和 β2 是衰减系数，分别控制动量项和均方根项的衰减程度
* ε 是平滑项

# 3 无梯度优化算法

### 3.1 进化算法

进化算法是一种受生物进化过程启发的优化算法，它通过模拟自然选择和遗传变异来寻找最优解。进化算法通常用于解决复杂、非凸的优化问题，在深度学习中也得到了广泛的应用。

#### 3.1.1 遗传算法

遗传算法（GA）是一种进化算法，它使用种群中的个体来表示候选解。每个个体由一组基因组成，这些基因代表了解的特征。GA通过以下步骤迭代地优化解：

1. **选择：**根据个体的适应度（目标函数值）选择个体进行繁殖。
2. **交叉：**随机选择两个父个体，交换它们的基因以创建新的子个体。
3. **变异：**随机改变子个体的基因，以引入多样性。
4. **精英保留：**将最优个体保留到下一代中。

**代码示例：**

import random

class GA:
    def __init__(self, population_size, gene_size, fitness_function):
        self.population_size = population_size
        self.gene_size = gene_size
        self.fitness_function = fitness_function
        self.population = self.generate_population()

    def generate_population(self):
        population = []
        for _ in range(self.population_size):
            gene = [random.randint(0, 1) for _ in range(self.gene_size)]
            population.append(gene)
        return population

    def fitness(self, gene):
        return self.fitness_function(gene)

    def select(self):
        fitness_values = [self.fitness(gene) for gene in self.population]
        probabilities = [fitness / sum(fitne